数学IAIIB 数学IA順列に関する問題の考え方 数学IAIIB 差をつける自宅学習を始めよう ここでは「順列」について説明します。 順列とは,いくつかあるものを順序をつけて1列に並べる配列のことです。 Contents 1 意味を考えて順列を求めるほかの記事を探す 分野別 レベル別 他 キーワードで検索する 数学の実力を試そう 入試数学コンテスト 物理の記事 高校生 高校数学の問題と解答の部屋 教科書の問題を質問!解説依頼ページ Site Information 「高校数学の知識庫」を今より10倍活用する方法 順列の問題 条件を言い換える 問題解説 スポンサーリンク 今回の問題はこちら 1から9までの数字から5個の数字をとって作った

高校数学 数a 勉強動画 順列 基本編の問題 19ch
数学 順列 問題
数学 順列 問題- 数学A 組合せ 同じものを含む順列特訓① 数学A 組合せ 最短経路特訓① スポンサードリンク Tweet;いまの問題で見たように,順列は樹形図を考えれば積の法則を使って計算できますね. 前回の記事:場合の数1|和の法則と積の法則は超アタリマエ! 和の法則と積の法則は場合の数の分野で最も基本的であり,他の公式などは全てこの2つの原理に帰着されます. 和の公式も積の



順列 P とは 公式や計算問題の解き方 重複ありなど 受験辞典
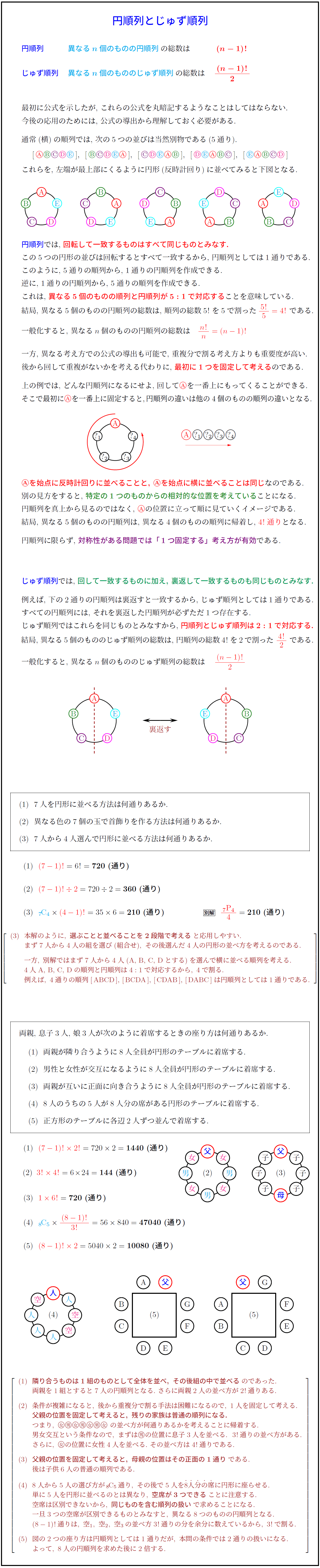
互いの位置関係だけが問題になります。 例として の 3 人が座る場合を考えると,上の図の 3 通りの座り方は, どれも から見て右回りに の順に座っているので同じ座り方になります。 このようなときには円順列の考え方を用います。 まず,誰でもよいので 1 人の座る位置を固定します。 父親の座る位置を固定すると,残り 5 人の座り方について考えることになり例 各位の数が異なる2桁の整数の総数 (解答) 10個の数字 0,1,2,3,4,5,6,7,8,9 から異なる2つを取って並べる順列 10 P 2 =10·9=90 のうち,先頭が0のもの(9個)は1桁になるから,909=81個 (別解) 十の位は0以外の9通り,それぞれ1の位は9通りだから,9×9=81通り 例 2桁の整数の総数 (解答) 10個の数字 0,1,2,3,4,5,6,7,8,9 から重複を許して2つを取って並べる順列 10Π2 =10 2 =100プリント問題 算数(復習),中1数学,中2数学,中3数学 数学まとめ 算数(復習),中1数学,中2数学,中3数学 高1数学 数検(準二級)対策,数Ⅰ(数と式),不等式,二次関数,三角比,順列・組合せ,確率 中1数学 中2数学 中3数学 中学100マス プリント問題 数学まとめ 高1数学 成績 名前記録 キャラ・コレ
設問1の解答と解説: ここは素直に公式を使うのが確実で一番早い。 順列と組合せの公式がごっちゃにならないように覚えましょう。 設問1は、『走る順番は何通りあるか? 』を問われているので順列の公式を使います。 nは、大人3人と子供4人の合計7人となります。 rは、合計7人の中から4人を選択するので、4人となります。 解答:C 練習問題 順列と組合せの問題を混ぜました。順列と組合せの違い 順列 :「選んで並べる」「abとba を区別してそれぞれ数える」 組合せ :「選ぶだけで並べない」「abとbaは区別せず同じもの」 に注意しながら,考えてみてください。 高校数学の授業内容を想定して,自宅で学習できるよう工夫したプリントです。毎日の授業の予習や復習に,自宅で自分ペースで学習したいとき等に活用してください。数学Ⅰ01 数と式( 準備中です )学習プリント( 準備中です )学習プリント
高校生・数学a場合の数・順列問題の基本を丁寧に解説!授業動画あり 高校生・数学a場合の数・順列問題の基本を丁寧に解説!授業動画あり 21 6/28 動画 授業 高校生 場合の数や確率って、中学校でも習いましたよね。 でも高校で習う場合の数・確率分野は 数学の疑問 順列と組み合わせの数の公式。どちらを使うのが正しいか迷ったときの便利なテクニック Tooda Yuuto 16年11月11日 / 19年9月9日 いま、「1」「2」「3」「4」「5」の5枚のカードがあるとします。 この5枚のカードについて、2種類の問題を考えてみましょう。 ①:「この中から2枚を数学で必ずやっておきたい復習チェックポイント&復習法 数学 比例とは? 入試問題 都立戸山高等学校16年度数学過去問大問4解説 数学 ひらめきに頼らず中学数学の図形問題を解く7つのコツ




北海道札幌厚別高等学校 数学応用 学校設定科目 順列 組合せの違いを理解する 竹之内 康秀教諭



Cl Bggoxxqdvdm
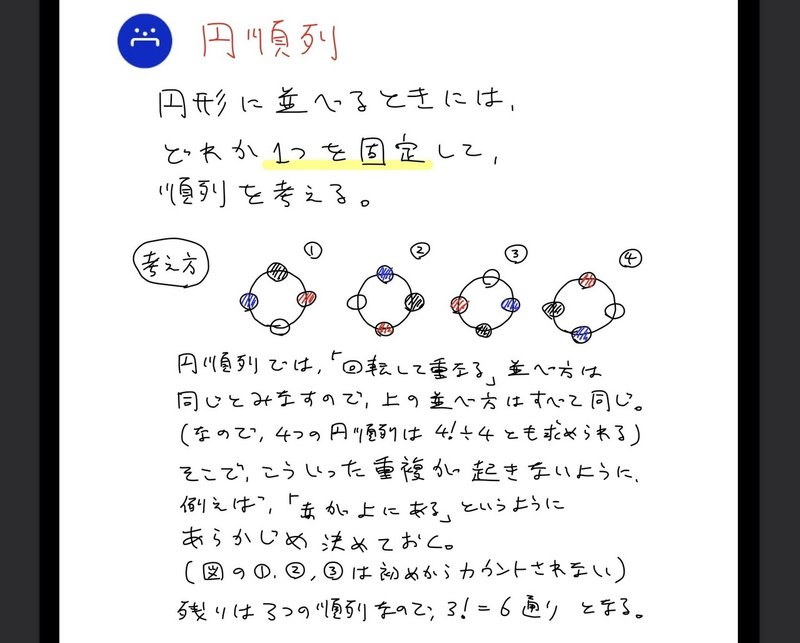
ただし,立方体を回転させて一致する塗り方は同じものとみなし,隣り合う面は異なる色を塗るものとする。 (1)赤,青,白,黒,緑,黄の6色 (2)赤,青,白,黒,緑の5色 (3)赤,青,白,黒の4色 (4)赤,青,白の3色 問題⑥ 正四角錐の5つの面を次のように塗る方法は何通りあるか。 ただし,回転させて一致する塗り方は同じものとみなし円順列の問題の考え方 例 黒,赤,青,緑の 4 4 色の玉を円状に並べるのは何通りか. 円順列の問題のポイントは, 回転して同じものは同じ並べ方としてみる という点にあります. それを踏まえると,以下の 6 6 通りになります. 問題を解く上で,回転されると手に負えないので, 回転を止めて考える のがポイントになります. 黒が上にあるときで固定して問題の図をクリックすると解答(pdfファイル)が出ます。 大学入試数学の問題の目次ページへ 毎日数学楽しみましょう! 入試問題募集中。受験後の入試問題(落書きありも写メも可) や質問等ありましたら 谷口美喜夫までメール をよろしくお願いします。 (氏名のところを長押しするとメール




高1 数学a 順列 組み合わせ 高校生 数学のノート Clearnote




3分で分かる 順列と組み合わせの違いと公式をわかりやすく 練習問題つき 合格サプリ
順列Pの公式と使い方を徹底解説! 5分で分かる順列のコツ! 「順列の公式ってなんだっけ? 」 今回は順列に関するこんな悩みを解決します。 順列の問題がすごく苦手なんですよ 数学Aでは順列や組み合わせを用いて事象の場合の数を求めます。 順列/ 数学公式集 / 順列 ワーク問題が分からなかった。3 ご意見・ご感想 nPrを使う問題でしたが、rが左端にくるには何通りあるか、という問題なので役にたたなかったです。 8 1303 30歳代 / 会社員・公務員 / 役に立った / 使用目的 オプションの総バリエーション数 9 1543いろいろな例題 順列に関する基本的なタイプの問題を $3$ 種類紹介します. 並べる順番を工夫する 例 $6$ 個の数字 $0,1,2,3,4,5$ から異なる $4$ 個を並べて,$5$ の倍数であるような $4$ 桁の整数は何個つくれるか. $4$ 桁の数字をつくる問題です.単純に選んだ数を左から並べるとする




3分で分かる 順列と組み合わせの違いと公式をわかりやすく 練習問題つき 合格サプリ



同じものを含む順列の問題 京極一樹の数学塾
組分け問題のパターン 高校数学における組分け問題は ・モノ(配られるもの)が区別できるか否か ・組(配属先)が区別できるか否か ・組(配属先)のモノの数に指定はあるか,指定がないならば,$0$ 個の組は許されるか 以上のカテゴリーによって以下のように分類されます. モノの区別 組の高校数学Aで学習する場合の数の単元から 「3桁、4桁の整数をつくる場合の数」 についてパターン別に解説していきます。 取り上げる問題はこちら! 問題①(0を含まないパターン) 6個の整数 隣り合う円順列の問題は まず $1$ つにまとめてしまい、円順列の総数を求める。 $1$ つにまとめたもの同士の並び替えの場合の数を求める。 積の法則より、掛け算すればok;




高校数学 1から分かる順列と組み合わせの違い 公式 問題付き 高校生向け受験応援メディア 受験のミカタ




順列pと組み合わせcの違いと 簡単 な見分け方
関連記事 高校数学 解説動画 数学A 整数の性質 すべての正の約数 さて今回から、素因数分解を使って解く問題をいくつか扱っていきます(`・ω・´) まずは、すべて 記事を読む 高校数学 順列の特訓プリントです(`・ω・´) 図を描くのが解くためのカギです(*´ω`*) 数学a 順列 人を並べる特訓① 数学a 順列 桁数問題特訓① 数学a 順列 辞書式配列・小さい順特訓① 数学a 順列 円順列(人を並べる)特訓①このサイトについて 以上で練習問題は終わりです。 順列と組み合わせは混同されやすいですが、慣れれば簡単に見分けられるので、いろいろな問題を解いて経験を積みましょう! コメントを残す コメントをキャンセル メールアドレスが公開されることはありません。 * が




円順列の応用問題5選 難問2選を解説 順列との違いとは 遊ぶ数学



順列 P とは 公式や計算問題の解き方 重複ありなど 受験辞典
練習問題 練習問題+解答 組合せの総数 n C r が整数であることの証明確率 例題(8) 練習問題 練習問題+解答整数の性質 例題(11) 練習問題 練習問題+解答図形の性質 例題(18) 練習問題 練習問題+解答 三角形の角の二等分線と比 メネラウスの定理,チェバの定理組合せの最も基本的な事柄と,よくある組合せの問題を解説します. 組合せとは いくつかのものからいくつかのものを取り出して並べることを順列と呼んでいました.ここでは,取り出したときの順序を考えない場合の数を考えてみましょう.そのような問題は組合せの問題と呼ばれています. 順列$\rightarrow$ 順序を考慮 (区別)する. 組合せ$\rightarrow$ 順序を考慮10個の数字 0,1,2,3,4,5,6,7,8,9 から異なる2つを取って並べる順列 10 p 2 =10·9=90 のうち,先頭が0のもの(9個)は1桁になるから,909=81個 (別解) 十の位は0以外の9通り,それぞれ1の位は9通りだから,9×9=81通り




数学ia 順列に関する問題の考え方 大学入試数学の考え方と解法




第6回 数学問題 順列を作る Dreamhanks Blog
以上 $3$ つです。 まとめて確認しましょう。 慣れないと難しく感じますが、確率の問題で、組合せと順列を入れ替えて解くと解きやすくなるケースがあるので、余力があれば身につけておきましょう。 広告 を始めました! なかけんの数学ノートのチャンネルができました。数学に関連する動画を定期的にアップ




15年10月 怜悧玲瓏 高校数学を天空から俯瞰する




高校数学 数a 勉強動画 順列 基本編の問題 19ch




順列と組み合わせの公式とその違い 問題付き 理系ラボ



円順列 数学入試問題




高校数学 1から分かる順列と組み合わせの違い 公式 問題付き 高校生向け受験応援メディア 受験のミカタ




順列と組み合わせの公式とその違い 問題付き 理系ラボ



円順列の応用問題 隣り合う 向かいあわせ と指示される問題 あうるさんの杜




高校数学 数a 勉強動画 順列 グループ分け編の問題 19ch



数学i Aチェック リピート 第7章 2順列 組合せ 8 同じものを含む順列 Pukiwiki




順列の問題 一定の条件で並べる 高校数学の知識庫




教科書レベルの問題一覧と解答 数学a 場合の数と確率 教科書より詳しい高校数学




リンゴ9個 重複組合せ 解説その1 知能問題 数的処理 判断推理 数的推理 数学パズル spi 空間把握 解いてみてください



3




高校数学 1から分かる順列と組み合わせの違い 公式 問題付き 高校生向け受験応援メディア 受験のミカタ




クリアー数学a 数a P99 4 円順列 重複順列



1



同じものを含む順列の問題 京極一樹の数学塾




数学a 完全順列もしくは ベルヌーイ オイラーの封筒取り違え問題 が面白い 青チャートと黄チャートの違い 学習村の 国公立へ行こう




教科書レベルの問題一覧と解答 数学a 場合の数と確率 教科書より詳しい高校数学




なぜ 同じものを含む順列の公式と使い方について問題解説 数スタ




円順列の応用問題5選 難問2選を解説 順列との違いとは 遊ぶ数学




高校生 順列のノート一覧 Clearnote




じゅず順列 おいしい数学



数学についてです 順列についてですが この問題は組み合わせでも解けま Yahoo 知恵袋



高校数学a 異なるものの円順列とじゅず順列 受験の月




改訂版 4step数学a P103 4 円順列 重複順列



3



同じものを含む順列の問題 京極一樹の数学塾




重複順列 部屋分け 数学a 場合の数 入試基本問題演習 Youtube




高校数学 数a 7 順列 基本編 Youtube



12 鹿児島大学 入試問題から Kadaiの順列




苦手な人向け 順列pの計算のやり方を簡単にサクッと解説するぞ 数スタ




場合の数 同じものを含む順列について 日々是鍛錬 ひびこれたんれん




順列と組合せの違いとその公式とは 応用問題5選もあわせて解説 遊ぶ数学



2




順列と組み合わせの数の公式 どちらを使うのが正しいか迷ったときの便利なテクニック アタリマエ



2




数珠順列とは 円順列との違いから練習問題まで 高校生向け受験応援メディア 受験のミカタ




Spi 数学 対策問題 組み合わせ 順列 しかくのいろは




高校数学 1から分かる順列と組み合わせの違い 公式 問題付き 高校生向け受験応援メディア 受験のミカタ




数学a 場合の数 順列の問題か 組み合わせの問題かの見分け方 坪田塾 公式youtubeチャンネル Youtube




高校数学a 同じものを含む順列 練習編 映像授業のtry It トライイット




高校数学a 円順列 練習編 映像授業のtry It トライイット




コンプリート 数学 確率 問題 ぬりえのベストコレクション




15年10月 怜悧玲瓏 高校数学を天空から俯瞰する




高校数学無料問題集 数a 第1章 場合の数と確率 順列 桝 ます Note



順列




同じものを含む順列の問題についてです この問題の のマーカーをした 数学 教えて Goo




円順列 おいしい数学



数学a順列組み合わせ この問題なぜここで終わってはいけないんですか なぜ Yahoo 知恵袋



数学の順列 組み合わせの問題です 6個の文字a A B C D Eから4個を Yahoo 知恵袋



高校数学a 重複順列の問題です 画像の問題です 1 の答案 Yahoo 知恵袋




高校数学a Npr と Ncr の使い分け 練習編 映像授業のtry It トライイット




同じものを含む円順列の裏技公式 高校数学の美しい物語



2




3講 順列 1章 場合の数と確率 問題集 高校数学a



確率問題全般 京極一樹の数学塾




高校数学a 辞書式に並べる順列 受験の月




高校数a 順列 の基礎を元数学科が解説する 苦手克服 ジルのブログ



高校数学無料問題集 数a 第1章 場合の数と確率 順列 桝 ます Note




3講 順列 1章 場合の数と確率 問題集 高校数学a



Lh3 Googleusercontent Com Proxy Hpejwlzfgmnxnz4n6pvabulsqqfwjv1yzijtoqqcs Lxsct9ckf5djccqr2ayyaq A07vz7thafbqihygsqd 6l12v2jmmkzmv5polwjlrbem6tvduhfxm7qqyvosmnygherer0dzysu Tknqynykxluj Srup3vks07t1tbvb W



2




高校数学a 順列の活用2 男女の並べ方 練習編 映像授業のtry It トライイット




高校数学 数a 勉強動画 順列 続 基本編の問題 19ch



数学完全順列 黄チャートの問題です 解説を読んでも理解出来 Yahoo 知恵袋



順列 P とは 公式や計算問題の解き方 重複ありなど 受験辞典



数学i Aチェック リピート 第7章 2順列 組合せ 10 最短経路 Pukiwiki




順列と組合せの違いと例題 高校数学の美しい物語




答え 円順列と確率 Piece Check 16 17 東大数学9割のkatsuyaが販売する高校数学の問題集




組み合わせの考え応用 最短経路選択問題をシミュレーターで理解しよう 数学入門




高校数学 数a 勉強動画 順列 男女編の問題 19ch




高校数学 数a 11 順列 数字の応用編 Youtube




順列の公式 証明と公式の意味 高校数学の知識庫



数学i Aチェック リピート 第7章 2順列 組合せ 1 重複順列 順列 Pukiwiki




3講 順列 1章 場合の数と確率 問題集 高校数学a



同じものを含む順列の問題 京極一樹の数学塾




順列 組み合わせ 階乗とは わかりやすくまとめてみた 数学 もんプロ 問題発見と解決のためのプログラミング




順列 数学a 高校1年生 1学期中間考査ワーク練習問題 赤城 ᐡᐤᐡ



順列と組み合わせの違いと見分け方 公式や練習問題 受験辞典




順列と組み合わせの公式とその違い 問題付き 理系ラボ




円順列 Twitter Search Twitter



確率問題全般 京極一樹の数学塾




重複順列とは 基本公式と解き方を解説 高校生向け受験応援メディア 受験のミカタ




重複順列の問題6選とは 公式よりも応用問題の解き方が大切です 遊ぶ数学




高校数学a 重複順列 例題編 映像授業のtry It トライイット




なぜ 同じものを含む順列の公式と使い方について問題解説 数スタ




この問題はなぜ順列の公式ではなく 組み合わせの公式で説いているのですか Clearnote




重複組合せ 組合せ 重複順列に関する問題 2018年度前期日程高知工科大学の入試問題 身勝手な主張



同じものを含む順列の確率の問題 京極一樹の数学塾



プレゼント交換会の数学 完全順列 理系男子の独り善がり




高校数学のサイコロの問題と順列の問題と順列の利用 Clearnote



0 件のコメント:
コメントを投稿